ALI BABA
Long times ago, there lived o poor wodcutter named Ali baba.
One day, Ali baba saw a band of
thieves. The thieves stopped in front of huge rock. suddenly the head thief
said “open sesame!” the rock slowly
rolled open. When the thieves left, Ali baba whent to the rock. He said, “open
sesame!”. When the rock rolled open, Ali baba went to the cave. He saw alot of
treasure in the cave. Ali baba brought back some of the treasure. His family
was happy to see the treasure and they became rich.
One day, Ali baba’s wife bought a
beautiful necklace. The head thief saw her, seeing that she was a rich lady and
he planned to rob her. The head thief went to Ali baba’s house. He disguised
him self as a traveller and asked Ali baba for a place to rest. Being kind, Ali
baba invited him for dinner. While they were having dinner, Ali baba’s maid, Morgiana,
heard noises behind the kitchen. The thieves had come to steal Ali baba’s
treasure! Morgiana tiptoed to the big jars where the thief was hidding! The
clever maid quickly poured hot oil into the jars. Then all the thieves died!
The head thief heard his men screaming and became frightened. He run out of Ali
baba’s house and was never seen again. Ali baba told the king about the
thieves. He also told him about his brave maid, Morgiana.
The next day, the king came to Ali
baba’s house for dinner. Morgiana danced for him and the king was very pleased.
The king liked morgiana as she was brave and clever. The king decided to make
morgiana as his daughter because he hadn’t children. Morgiana was very happy.
Finally, Morgiana became a princess.
And what about the strange cave? Nobody know
since Ali baba has been inside it and became rich.
THE END
Translate:
Pada zaman dahulu kala,hiduplah
seorang pemotong kayu miskin yang bernama Ali baba.
Suatu hari, Ali baba melihat
segerombolan pencuri. Pencuri-pencuri tersebut berhenti di depan sebuah batu
yang sangat besar. Tiba-tiba seorang pimpinan dari pencuri itu berkata
“terbukalah!” batu besar itu perlahan-lahan terbuka. Ketika para pencuri itu
pergi, Ali baba pergi ke batu besar tersebut lalu brkata “terbukalah!” Ali baba
segera masuk ke dalam gua tersebut. Dia melihat banyak harta karun disana. Ali
baba membawa beberapa harta karun tersebut untuk keluarganya. Keluarganya
sangat bahagia dan mereka menjadi orang kaya.
Suatu hari, istri Ali baba membeli
sebuah kalung yang sangat indah. Pimpinan pencuri tadi melihatnya, ia berencana
merampok istri Ali baba karena ia berpikir bahwa dia adalah orang kaya. Pimpinan
pencuri itu pergi ke rumah Ali baba. Dia menyamar sebagai seorang pelancong dan
bertanya kepada Ali baba tempat untuk menginap. Karena Ali baba orang yang
sangat baik, maka ia mengundangnya untuk makan malam di rumahnya. Ketika mereka
berdua sedang makan malam, pembantu Ali baba yang bernama Morgiana mendengar
suara-suara aneh di belakang dapur. Para pencuri itu telah datang untuk
merampok harta Ali baba. Morgiana berjalan perlahan-lahan menghampiri
gentong-gentong besar taempat para pencuri itu bersembunyi lalu menuangkan
minyak yang panas ke dalam gentong-gentong tersebut dan akhirnya para pencuri itu
mati. Pimpinan pencuri itu mendengar teriakan anak buahnya maka ia pun lari
ketakutan dan sejak saat itu ia pun tidak pernah muncul lagi. Ali baba
menceritakan tentang para pencuri itu kepada raja. Dia juga menceritakan
tentang keberanian pembantunya Morgiana.
Keesokan harinya, sang raja datang
ke rumah Ali baba untuk makan malam. Morgiana menari untuk raja, sang raja
menjadi sangat tersanjung. Sang raja sangat suka dengan Morgiana karena ia
sangat berani dan pandai. Sang raja tidak mempunyai anak maka ia memutuskan
untuk mengankat Morgiana menjadi anaknya. Morgiana menjadi sangat bahagia.
Akhirnya, Morgiana menjadi seorang
putri raja. Dan bagaimana dengan gua yang aneh itu? Tidak seorangpun
mengetahuinya sejak Ali baba masuk ke dalamnya dan menjadi orang yang sangat
kaya.
SELESAI^^



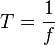
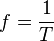

 , dengan k = tetapan pegas (N / m)
, dengan k = tetapan pegas (N / m) dan
dan  . Secara umum, konstanta total pegas yang disusun seri dinyatakan dengan persamaan :
. Secara umum, konstanta total pegas yang disusun seri dinyatakan dengan persamaan : , dengan kn = konstanta pegas ke - n.
, dengan kn = konstanta pegas ke - n.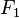 dan
dan 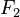 , pertambahan panjang sebesar
, pertambahan panjang sebesar 
 tergantung pada seutas kawat halus sepanjang
tergantung pada seutas kawat halus sepanjang  dan massanya dapat diabaikan. Apabila bandul itu bergerak vertikal dengan membentuk sudut
dan massanya dapat diabaikan. Apabila bandul itu bergerak vertikal dengan membentuk sudut  , gaya pemulih bandul tersebut adalah
, gaya pemulih bandul tersebut adalah  . Secara matematis dapat dituliskan :
. Secara matematis dapat dituliskan :
 , maka :
, maka :

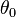 , maka persamaan gerak harmonik sederhana menjadi
, maka persamaan gerak harmonik sederhana menjadi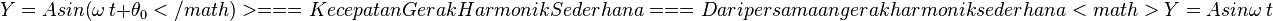

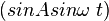
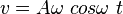
 atau
atau  , sehingga :
, sehingga : 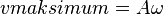
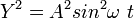 , maka :
, maka :
 ...(1)
...(1)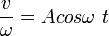 ...(2)
...(2)
 = kecepatan sudut
= kecepatan sudut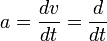
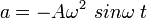
 atau
atau  = 900 =
= 900 = 

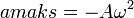

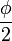 atau kita dapat memandang Gerak Harmonik Sederhana sebagai suatu komponen Gerak Melingkar Beraturan. Jadi dapat diimpulkan bahwa pada suatu garis lurus, proyeksi sebuah benda yang melakukan Gerak Melingkar Beraturan merupakan Gerak Harmonik Sederhana. Frekuensi dan periode Gerak Melingkar Beraturan sama dengan Frekuensi dan periode Gerak Harmonik Sederhana yang diproyeksikan.
atau kita dapat memandang Gerak Harmonik Sederhana sebagai suatu komponen Gerak Melingkar Beraturan. Jadi dapat diimpulkan bahwa pada suatu garis lurus, proyeksi sebuah benda yang melakukan Gerak Melingkar Beraturan merupakan Gerak Harmonik Sederhana. Frekuensi dan periode Gerak Melingkar Beraturan sama dengan Frekuensi dan periode Gerak Harmonik Sederhana yang diproyeksikan.
 ... (1)
... (1) ... (2), x adalah jarak linear, v adalah kecepatan linear dan t adalah waktu tempuh (x = vt adalah persamaan Gerak Lurus alias Gerak Linear). Kemudian v pada persamaan 2 digantikan dengan v pada persamaan 1 dan jari-jari r digantikan dengan A :
... (2), x adalah jarak linear, v adalah kecepatan linear dan t adalah waktu tempuh (x = vt adalah persamaan Gerak Lurus alias Gerak Linear). Kemudian v pada persamaan 2 digantikan dengan v pada persamaan 1 dan jari-jari r digantikan dengan A :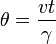

 ... (3) (
... (3) ( ...(4)
...(4)


